(This is a draft and truncated version - for final and full version, see
Concise Encyclopedia of Biostatistics for Medical Professionals)
half-life of medications
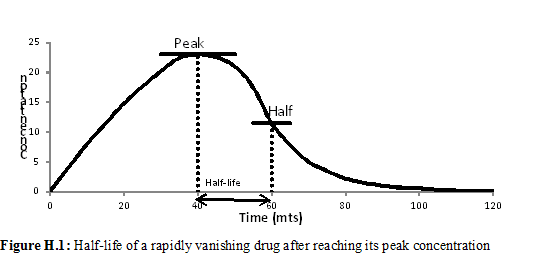
When a drug is ingested, it may reach its peak concentration in the system gradually but then starts to decay quickly, or may reach the peak quickly and starts decaying slowly. Half-life is the time taken to go from the peak concentration to half that concentration. Figure H.1 shows half-life for a drug that reaches its peak gradually but decays quickly. Half-life is utilized to measure the duration that a drug remains in the system and may form the basis for prescribing the periodicity (once-a-day, twice-a-day, etc.) of intake. For example, Schulze-Bonhage and Hintz [1] suggested that the anti-epileptic drug perampenal can be prescribed once daily because of its long half-life.
If half-life of a drug is 3 hours, it reduces to one-half of its peak concentration in 3 hours. It does not mean it will vanish in the next 3 hours. After 6 hours, the drug concentration will be one-half of what it was at 3 hours, i.e., one-fourth of the peak concentration; and after 9 hours it will be one-eighth of its peak concentration. It takes more than 4 half-lives to reduce the concentration to less than 5% of its peak concentration. After this, the concentration will not vanish but tends to stabilize. A rule-of-thumb says that it takes about four times the half-life of the drug for the concentration of that drug in the system to reach a steady state irrespective of the half-life. So if you administer a drug with a half-life of 12 hours, the steady state will be achieved after 48 hours. Drugs with short half-life reach to a steady state relatively quickly compared with those with long half-life. An example of the statistical use of half-life is in the field of crossover trials. For a usual crossover experiment to be successful there must be no carryover effect. The time required for the carryover effect to vanish is called the washout period. This should generally be at least four times the half-life of the substance to be confident there is only negligible amount of the substance in the system.
Half-life is obtained by fitting a regression of concentration on time and locating the time point where concentration is one-half of the peak. In most pharmacologic applications, concentration decline is fast in the beginning and increasingly slow later on, which suggests that a log-scale is appropriate. Hence a linear regression of log(concentration) vs. time is generally used. If the slope of this line is b,
Half-life: T½ = . ... ...
For final and full version, see
Concise Encyclopedia of Biostatistics for Medical Professionals
Concise Encyclopedia of Biostatistics for Medical Professionals)
half-life of medications
When a drug is ingested, it may reach its peak concentration in the system gradually but then starts to decay quickly, or may reach the peak quickly and starts decaying slowly. Half-life is the time taken to go from the peak concentration to half that concentration. Figure H.1 shows half-life for a drug that reaches its peak gradually but decays quickly. Half-life is utilized to measure the duration that a drug remains in the system and may form the basis for prescribing the periodicity (once-a-day, twice-a-day, etc.) of intake. For example, Schulze-Bonhage and Hintz [1] suggested that the anti-epileptic drug perampenal can be prescribed once daily because of its long half-life.
If half-life of a drug is 3 hours, it reduces to one-half of its peak concentration in 3 hours. It does not mean it will vanish in the next 3 hours. After 6 hours, the drug concentration will be one-half of what it was at 3 hours, i.e., one-fourth of the peak concentration; and after 9 hours it will be one-eighth of its peak concentration. It takes more than 4 half-lives to reduce the concentration to less than 5% of its peak concentration. After this, the concentration will not vanish but tends to stabilize. A rule-of-thumb says that it takes about four times the half-life of the drug for the concentration of that drug in the system to reach a steady state irrespective of the half-life. So if you administer a drug with a half-life of 12 hours, the steady state will be achieved after 48 hours. Drugs with short half-life reach to a steady state relatively quickly compared with those with long half-life. An example of the statistical use of half-life is in the field of crossover trials. For a usual crossover experiment to be successful there must be no carryover effect. The time required for the carryover effect to vanish is called the washout period. This should generally be at least four times the half-life of the substance to be confident there is only negligible amount of the substance in the system.
Half-life is obtained by fitting a regression of concentration on time and locating the time point where concentration is one-half of the peak. In most pharmacologic applications, concentration decline is fast in the beginning and increasingly slow later on, which suggests that a log-scale is appropriate. Hence a linear regression of log(concentration) vs. time is generally used. If the slope of this line is b,
Half-life: T½ = . ... ...
For final and full version, see
Concise Encyclopedia of Biostatistics for Medical Professionals
