(This is a draft and truncated version - for final and full version, see
Concise Encyclopedia of Biostatistics for Medical Professionals)
Mauchly test for sphericity
The Mauchly test assesses the validity of the sphericity assumption that underlies univariate repeated measures analysis of variance (ANOVA). It was developed by John Mauchly in the year 1940 [1]. We first explain sphericity and then describe Mauchly test.
John Mauchly (Photo)
Sphericity in Repeated Measures
In repeated measures, sphericity is the equality of variances of the differences in values observed at different points in time. As usual, this refers to the population parameters rather than to the sample values. Repeated measures ANOVA uses these differences and such homogeneity is required for valid results. Note that the concept of sphericity applies only when you have three or more repeated values. If you have just two repetitions, there is only one difference, and the question of sphericity does not arise.
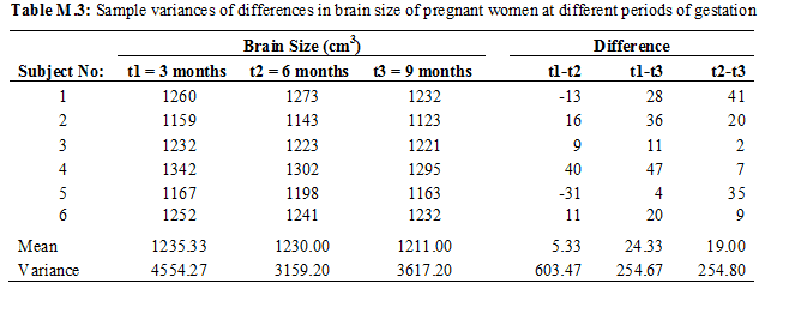
Suppose brain size of pregnant women [2] is measured by MRI at 3 months, 6 months and 9 months of pregnancy to find if pregnancy affects the brain size. Let the values obtained be as in Table M.3. The differences and their variances are also shown in the table. Sphericity is about equality of variances at the bottom of the last three columns. In this example, the variance of the difference in brain size between 3 months and 9 months, and between 6 months and 9 months are nearly same but the variance of difference between 3 months and 6 months is large. Thus, the sphericity condition is not likely to be valid for repeated measures ANOVA in these data.
The sphericity can also be studied by the correlation structure of the values obtained at different time-points. This is sometimes confused with compound symmetry where not just the covariances between values at different time points are the same but the variances of values at different time points are also the same. This is more than required for sphericity. Sphericity requires same variances of the differences but not the same variances of the values at different time points. In other words, compound symmetry is sufficient for sphericity but not necessary.
Let us also mention as a side note that sphericity is the requirement for repeated measures ANOVA when univariate methods are used and not for multivariate methods. Univariate method is advised when the sample size is relatively small (say, n < K +10, where K is the number of repeated measures), unequal from group to group, and sphericity is not violated. There is another twist to the story. When sphericity is violated, the univariate solution is to reduce the degrees of freedom (df) by what is called Huynh-Feldt correction or similar other corrections. This correction is a multiplier less than equal to 1, called ε, and depends on the extent of lack of sphericity in the data—more is the departure, the more is the correction. The mean squares and other calculations including the actual value of the F-statistic remain the same, only the df changes. This reduction in df increases the critical value and thus adjusts the Type-I error to the correct level for lack of sphericity. Since this correction to the df is available, you can directly use this correction without going through the process of checking the validity of sphericity in your data. This makes Mauchly test redundant but is still commonly used for medical data. ... ...
The Mauchly Test
The computational formula for Mauchly test is complex that we wish to avoid. However, this is the default test of sphericity in several common statistical software programs. You should not have any difficulty in using this test when needed. This follows a chi-square distribution with df where K is the number of repeated measures. Note that K(K – 1)/2 is the number of pairwise differences when the measurement is repeated K times.
The validity condition of Mauchly test includes multivariate Gaussian (Normal) distribution of the data, and the test is not robust to nonGaussianity. If the data do not have Gaussian pattern, think of some transformation before using the Mauchly test. In that case, the repeated measures ANOVA will also be on the transformed values. The other limitation of Mauchly test is ... ...
For final and full version, see
Concise Encyclopedia of Biostatistics for Medical Professionals
Concise Encyclopedia of Biostatistics for Medical Professionals)
Mauchly test for sphericity
The Mauchly test assesses the validity of the sphericity assumption that underlies univariate repeated measures analysis of variance (ANOVA). It was developed by John Mauchly in the year 1940 [1]. We first explain sphericity and then describe Mauchly test.
John Mauchly (Photo)
Sphericity in Repeated Measures
In repeated measures, sphericity is the equality of variances of the differences in values observed at different points in time. As usual, this refers to the population parameters rather than to the sample values. Repeated measures ANOVA uses these differences and such homogeneity is required for valid results. Note that the concept of sphericity applies only when you have three or more repeated values. If you have just two repetitions, there is only one difference, and the question of sphericity does not arise.
Suppose brain size of pregnant women [2] is measured by MRI at 3 months, 6 months and 9 months of pregnancy to find if pregnancy affects the brain size. Let the values obtained be as in Table M.3. The differences and their variances are also shown in the table. Sphericity is about equality of variances at the bottom of the last three columns. In this example, the variance of the difference in brain size between 3 months and 9 months, and between 6 months and 9 months are nearly same but the variance of difference between 3 months and 6 months is large. Thus, the sphericity condition is not likely to be valid for repeated measures ANOVA in these data.
The sphericity can also be studied by the correlation structure of the values obtained at different time-points. This is sometimes confused with compound symmetry where not just the covariances between values at different time points are the same but the variances of values at different time points are also the same. This is more than required for sphericity. Sphericity requires same variances of the differences but not the same variances of the values at different time points. In other words, compound symmetry is sufficient for sphericity but not necessary.
Let us also mention as a side note that sphericity is the requirement for repeated measures ANOVA when univariate methods are used and not for multivariate methods. Univariate method is advised when the sample size is relatively small (say, n < K +10, where K is the number of repeated measures), unequal from group to group, and sphericity is not violated. There is another twist to the story. When sphericity is violated, the univariate solution is to reduce the degrees of freedom (df) by what is called Huynh-Feldt correction or similar other corrections. This correction is a multiplier less than equal to 1, called ε, and depends on the extent of lack of sphericity in the data—more is the departure, the more is the correction. The mean squares and other calculations including the actual value of the F-statistic remain the same, only the df changes. This reduction in df increases the critical value and thus adjusts the Type-I error to the correct level for lack of sphericity. Since this correction to the df is available, you can directly use this correction without going through the process of checking the validity of sphericity in your data. This makes Mauchly test redundant but is still commonly used for medical data. ... ...
The Mauchly Test
The computational formula for Mauchly test is complex that we wish to avoid. However, this is the default test of sphericity in several common statistical software programs. You should not have any difficulty in using this test when needed. This follows a chi-square distribution with df where K is the number of repeated measures. Note that K(K – 1)/2 is the number of pairwise differences when the measurement is repeated K times.
The validity condition of Mauchly test includes multivariate Gaussian (Normal) distribution of the data, and the test is not robust to nonGaussianity. If the data do not have Gaussian pattern, think of some transformation before using the Mauchly test. In that case, the repeated measures ANOVA will also be on the transformed values. The other limitation of Mauchly test is ... ...
For final and full version, see
Concise Encyclopedia of Biostatistics for Medical Professionals
